Propagación del coronavirus COVID19 en México (Con ecuaciones diferenciales)

Hace unos días publicamos este post en cual mediante el uso de ecuaciones diferenciales explicamos el proceso de propagación del coronavirus COVID19, y mostramos la importancia de controlar y reducir el riesgo de contagio. A continuación, mostraremos graficas con datos actualizados. El contenido original del post se encuentra después de las gráficas actualizadas.

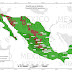
Casos de Coronavirus COVID19 en México al 01 de Abril de 2020

Ya suman 1215 casos, y 29 fallecidos en México a causa del coronavirus COVID19. En otro post presentamos mapas donde se puede visualizar la distribucion geograficas de dichos casos.

Como mencionamos anteriorment (ver final del post), el riesgo de infección por coronavirus COVID19 parece estabilizarse en 0.20.

riesgo de contagio de COVID19 en Mexico

Sin embargo, el dato preocupante es el de la tendencia en el número de muertos, pues parece ser una tasa de aumento superior a la del contagio.

Casos de COVID19 en Mexico y muertes por COVID19

La ecuacion diferencial del coronavirus COVID19 para México

La pandemia del coronavirus COVID19 tomo por sorpresa al mundo, y se expandió de forma inesperada. Muchos países tomaron medidas de emergencia como cerrar sus fronteras, declarar cuarentenas o toques de queda.

Existe mucha incertidumbre sobre como aumentaran los casos en México, y si dichas medidas son razonables o no.

En este post utilizaremos ecuaciones diferenciales (de forma simple) para explicar la propagación del virus y la importancia de controlar el riesgo.

La ecuación diferencial del coronavirus COVID19

y(t) = casos de coronavirus en el instante t. Es función del tiempo “t”

y(t+Dt) = casos de coronavirus en el futuro t+Dt

La base de la epidemiologia matemática nos dice que la propagación de enfermedades infecciosas es proporcional al riesgo de infección R y al tiempo transcurrido

y(t+Dt) = y(t) + y(t) R Dt

Ordenando tenemos:

[Y(t+Dt) – y(t)]/Dt = R y(t)

Analizando cuando Dt es pequeño; es decir, cuando tiende a cero (0), vemos que el término de la izquierda nos recuerda el concepto matemático de límites, que es igual a la derivada de dicha función.

Lim [Y(t+Dt) – y(t)]/Dt = dy/dt

Dy/dt = R y

Lo cual nos muestra que tenemos una ecuación diferencial simple, que puede ser resuelta por separación de variables.

Dy/y = R dt

Integrando tenemos:

Ln(y) = Rt + c1

Por propiedad de logaritmos tenemos:

y(t) = exp (Rt) * exp(c1)

y(t) = C exp (Rt)

Nuestra condición inicial es el paciente 0; el primer contagio cuando el tiempo es 0, es decir, y (0) =1.

y (0) = C exp(R*0)

C = 1

Así, la ecuación es:

y(t) = exp (Rt)

Donde R es el riesgo de infección. El valor de R depende de muchos factores como ser:

• Exposición. Que tan expuestos estamos al contagio. Si salimos y estamos en contacto con personas infectadas, nos exponemos mas y el riesgo aumenta. Si no nos lavamos las manos ni usamos barbijo, también nos exponemos y el riesgo aumenta.
• Vulnerabilidad. Las personas mayores y las personas con un sistema inmunológico más débil son más vulnerables y corren mayor riesgo.

En este post no entraremos mucho al detalle teórico del riesgo, sino que utilizaremos una simplificación. De la ecuación tenemos que:

R = ln (y)/t

Como tenemos datos diarios sobre el número de infectados por día, podemos graficar la variación diaria del riesgo. La figura 1 nos muestra que el riesgo R tiende a un valor cercano a 0.2. Así, la ecuación será:

y(t) = exp (0.2t)

Figura 1

La importancia del riesgo de contagio

Para ver la importancia de disminuir el riesgo, haremos una simple prueba de sensibilidad considerando 3 casos:

• Escenario en que el riesgo disminuye a 0.18
• Escenario en que el riesgo se mantiene constante en 0.20
• Escenario en que el riesgo se incrementa a 0.22

Según estos 3 escenarios, el numero de infectados para el día 50 (16 de abril) seria:

• Riesgo 0.18: 8 104 casos
• Riesgo 0.20: 22 027 casos
• Riesgo 0.22: 59 875 casos

Este simple ejercicio matemático nos muestra la importancia de controlar y disminuir el riesgo. Pequeñas medidas que modificarían el riesgo en 0.02 pueden hacer la diferencia entre 8 000 y 59 000 casos (una diferencia de 41 000 casos de COVID19).

Nota. Si bien este articulo no se relaciona ni con satélites ni geografía ni sistemas de información geográfica, nos parece importante incluirlo en el blog debido a la emergencia de la pandemia coronavirus COVID19.